Neural network quantization is a process of reducing the precision of the weights in the neural network, thus reducing the memory, computation, and energy bandwidths.
Particularly when deploying NN models on mobile or edge devices, quantization, and model compression in general, is desirable and often the only plausible way to deploy a mobile model as the memory and computational budget of these devices is very limited.
Why not use potential infinite virtual memory and computational power from cloud machines? While a lot of NN models are running on the cloud even now, latency is not low enough for mobile/edge devices, which hinders utility and requires data to be transferred to the cloud which rises a lot of privacy concerns.
Preliminaries of Neural Network Quantization
There are a lot of quantization methods in the literature today and to best understand the pros and cons of each method it helps to classify quantization methods. Quantization in a general sense is assigning a discrete value from a pre-specified set of values for a given input.
Quantization-aware training vs. post-training quantization
When the quantization operations are embedded into a neural network and then trained it is called quantization-aware training. And if quantization is performed on a model after training, for example with rounding mechanisms, it is called post-training quantization.
Scalar quantization vs. vector quantization vs. product quantization:
If the input is scalar and the pre-specified set is also a scalar, then it is called scalar quantization (for example, making FP32 floating point into INT8 integer). If the input is a vector and it is assigned to a vector, it is called vector quantization. Product quantization is a form of vector quantization with increased granularity as it works with sub-vectors rather than the entire vector.
Unified quantization or non-unified quantization:
During quantization, if there is a restriction that discrete values that can be assigned should be at equal step size, then it is called unified quantization. Converting FP32 to INT8 is an example of unified quantization. Alternately, if the discrete set of values to be assigned doesn’t have any restrictions it is called non-unified quantization. Vector quantization and product quantization are examples of this type.
Fixed-precision quantization vs. mixed-precision quantization:
If different layers or channels have different precisions or bit-widths then it is called mixed-precision quantization. If the entire network is quantized to values of one bit-width, then it is called fixed-precision quantization.
Layer-wise quantization or channel-wise quantization:
This is a fine-grained classification within mixed-precision quantization depending on whether we have different bit-widths for each layer or for each channel.
Now we’ll dive into six research papers that addressed these problems in 2020.
And the Bit Goes Down: Revisiting the Quantization of Neural Networks (ICLR 2020)
Outstanding problem: State-of-the-art deep learning models take a lot of memory. Even ResNet-50, which is not quite state-of-the-art takes ~100MB and the Faster-RCNN takes ~200MB.
Compressing the model alone is desirable to deploy deep learning solutions in low-memory environments.
Proposed solution: This work proposes applying Product Quantization (PQ) to the weights of the network which represent the whole network with very few floating-point numbers.
Product Quantization: First, the columns of the M x N matrix are each split into d sub-vectors. It results in a total of M*d sub-vectors. These vectors are grouped into clusters, sometimes while minimizing a pre-specified loss. Then, to compress the matrix, these sub-vectors are replaced with the centroid of the cluster in which it falls. This achieves a stark compression as we store only cluster centroid vectors and cluster labels for sub-vectors rather than storing all the sub-vectors in a matrix.
This work applies the same process for weight matrix at each convolutional layer which is of size (C_out x C_in x K x K) where C_out and C_in are the number of channels going out of a layer and the number of channels coming into a layer and K is the height and width of a square kernel.

First, the weight matrix is reshaped to a 2d matrix where the size becomes (C_out x C_in*K*K). Columns of the weight matrix of length C_in*K*K are transformed into C_in sub-vectors each of K*K length. This results in C_out*C_in sub-vectors.
The labels of the sub-vectors are learned with weighted k-means with an objective of reducing the offset (reconstruction loss) between activations produced by the original weight matrix and the activations produced by a matrix created by replacing all the sub-vectors with their cluster centroids.
(They also show that reconstructing the activations of a layer is more efficient than reconstructing the actual weights of the network.)
Results and conclusion: It is shown that models could be compressed efficiently with this approach compared to the existing methods.

Also, a ResNet-50 model is quantized to a size of 5 MB (with 20x compression factor) and Mask R-CNN to a size of ~6MB (26x compression factor) both with competitive performances compared to the original models.


AutoQ: Automated Kernel-Wise Neural Network Quantization
Outstanding problem: Kernel-wise quantization (different bit-widths for each kernel) is shown to be more effective than layer-wise quantization which is in turn shown to be more effective than network-wise quantization.

As the search for space of all possible combinations is huge, manual engineering of kernel-wise bit-widths is sub-optimal. It is shown that even a generic RL agent like DDPG can’t find a good-enough policy. This work proposes a method that learns kernel-wise bit-widths more efficiently than any other existing method.
Proposed solution: This work proposed a Hierarchical Reinforcement Learning method to first choose layer-wise bit-widths with a High-Level Controller and then choose kernel-wise bit-widths with a Low-Level Controller within that layer.
HLC chooses bit-width for activations of a particular layer and also the mean bit-widths of all the kernels (termed as ‘goal for LLC’) of that layer. LLC then chooses bit-widths for all the kernels in that particular layer.

The reward for this HRL agent in training is devised such that the number of FLOPs and memory required is lower and test accuracy is higher.
To accelerate training, LLC is given an additional intrinsic reward, when it completes the goal set by HLC or chooses the bid-widths for kernels such that the mean is equal to the predicted mean of the HLC for that particular layer.
Results and conclusion: The proposed method outperforms previous RL methods like DDPG. It outperforms HIRO as well, even though their implementation is based on HIRO because of the intrinsic reward they designed for the LLC.

They also show that kernel-wise quantization is the right granularity to choose bit-widths with an experiment showing that sub-kernel-wise quantization doesn’t improve latency (inference time) beyond kernel-wise quantization.

Differentiable Product Quantization for End-to-End Embedding Compression
Outstanding problem: The embedding layer alone has 95% of all parameters in a medium-sized LSTM with the vocabulary of a language modeling dataset PTB.
Compressing the embedding layers without loss in performance of a model would make them mobile and edge-device friendly.
Proposed solution: This method adopts the Product Quantization (PQ) method where columns of a matrix are split into sub-vectors, clustered, and finally are replaced with the centroid sub-vectors of the cluster they belong to.

The notable aspect of this method is that it makes PQ differentiable by approximating the non-differentiable operators with Stop Gradient operators.
Given a weight matrix to compress (Query Q) the proposed method learns a codebook that contains the centroid vectors for each cluster and also the cluster labels for each sub-vector. At inference, this codebook is used to revert back the discrete representation (a list of cluster labels for each column) to a continuous vector representation.
Results and conclusion: The proposed method outperforms recently proposed embedding compression methods.

Also, it outperforms traditional embedding compression approaches like scalar quantization, product quantization (standard), and low-rank approximation.

Towards Accurate Post-training Network Quantization via Bit-Split and Stitching
Outstanding problem: Quantizing the neural network before training or while training (Quantization-aware training; with quantized operations embedded in the network) has to device special mechanisms for back-propagating through discrete quantized entities and needs domain expertise for hyperparameter tuning and also can’t work with models that are already trained.
On the other hand, post-training quantization avoids all of that but is shown to be ineffective for bit-widths lower than 8. TF-Lite is the previous state-of-the-art method that only uses 8-bit post-training quantization.
Proposed solution: This work proposes an optimization process to calibrate the network with a few unlabeled data and find the optimal low-bit integers to replace the floating-point values in the weight tensors. If the bit-width desired is m, the task is to find the best possible m-bit integer [-2^m-1, +2^m-1] for every floating-point FP32 weight in the weight matrix of a layer (so that it doesn’t result in performance degradation).
As this calibration process has a lot of search-space to optimize over, this work proposes to break the m-bit optimization process into m bits and then perform the more tractable optimization step of these individual bits.

After the optimization, which could be analytically performed after sensible assumptions, the bits are stitched back by adding all the bits multiplied with their associated power 2 terms. Hence, this process is called bit-split and stitching.
Results and conclusion: Compared to the previous state-of-the-art methodology of TF-Lite, the proposed method is effective in the 3-bit quantization of a network on the ImageNet dataset.

The proposed method also outperforms many recent methods for post-training quantization.

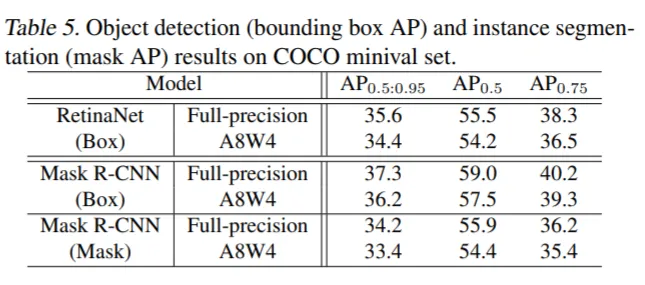
Also, the proposed method achieves 4-bit weight quantization and 8-bit activation quantization of RetinaNet and Mask-RCNN for object detection and segmentation with only 0.8–1.2% mAP degradation.
Bayesian Bits: Unifying Quantization and Pruning
Outstanding problem: Learning channel-wise bit-widths to perform adaptive quantization is very hard. Reinforcement learning and hierarchical reinforcement learning approaches have tried to learn effective strategies but they are not effective enough. This work learns channel-wise bit-widths effectively.
Also, if one needs to perform both quantization and pruning, methods that unify both are more effective than applying separate methods one-by-one. This work unifies both quantization and pruning.
While a lot of mixed-precision quantization methods find arbitrary bit-widths for each weight tensor, thus making the network incompatible with standard GPU/TPU accelerators, the proposed method comes up with strategies with only powers-of-two bit-widths, making it hardware friendly.
Proposed solution: First, this work proposes a formulation of M-bit quantization value as the addition of (M/2)-bit quantization value and M-bit residual error between (M/2)-bit quantization value and M-bit quantization value. Similarly, the (M/2)-bit quantization value can also be decomposed in terms of (M/4)-bit quantization value and the residual error between (M/2)-bit value and (M/4)-bit value.
Starting with 2-bit quantization, this decomposition allows for having binary gates that control whether to go for a higher bit-width or not, thus creating a mixed-precision strategy. This method learns this mixed-precision strategy, i.e., binary gates for each weight tensor in a variational inference framework with a few sensible approximations.

By starting with 0-bit quantization (practically pruning) this method unifies quantization and pruning in an effective way.
Results and conclusion: The proposed method outperforms many existing fixed-precision and mixed-precision methods on MNIST and CIFAR-10 datasets.

Also, it outperforms the existing state-of-the-art methods on the ImageNet dataset with ResNet-18 and MobileNet V2 architecture.

Up or Down? Adaptive Rounding for Post-Training Quantization
Outstanding problem: It has been previously shown that when quantizing a value from higher precision to lower precision, the rounding mechanism used has a lot of impact on performance.
Specifically, the performances of quantization with the nearest-value rounding mechanism, always ceiling or always flooring rounding mechanism, and stochastic rounding mechanism show a lot of variances. See the figure below.
(Stochastic rounding is a mechanism of rounding a value to a lower-precision value with the probability of (1- px) where px is the proximity of that particular value and the lower-precision value.)

This work proposes a better rounding mechanism post-training with just a small calibration on a few unlabelled examples.
Proposed solution: This work investigated whether to round up or round down for each weight by formulating it as an optimization problem of reducing the reconstruction loss of weights of a network.
This work set out to make the inherently discrete optimization problem into a continuous optimization problem with better formulations and sensible approximations based on Taylor series expansion.
Results and conclusion: The proposed (seemingly simple) method shows considerable effectiveness at post-training quantization and outperforms existing post-training quantization methods.

The authors also show that the effectiveness of their method increases with the number of unlabeled examples used for calibration across different datasets.

Conclusion
Research on Neural Network Quantization, more generally NN compression, is evolving to be more scientific and rigorous. One of the reasons is, undoubtedly, the interaction between the wide adoption of deep learning methods in Computer Vision & NLP and elsewhere and the increasing amount of memory, energy, and computational resources required for the state-of-the-art methods.
Because of the research in NN Quantization in 2020, we have different methods for layer-wise, channel-wise quantization methods rather than network-wise quantization methods, we have better post-training quantization techniques which are better than methods offered by TF-Lite, and we have approaches that combined pruning and quantization under one framework and give the advantages of both the techniques.
Going into the future we will see these advanced and efficient methods made more accessible to developers and researchers by including them into tools like TF-Lite and other NN compression libraries.
And it is exciting to see the research on this topic in 2021 which has to beat already great efficient approaches introduced this year.

Comments 0 Responses