Latest news about AI and ML such as ChatGPT vs Google Bard
Did you know that 60% of newly-launched products may not perform well because they fail to represent or actually offer something, their customers really want?
This is the era of personalization. Using personalization you can efficiently attract new customers and retain existing customers. These days, a one-size-fits-all approach generally doesn’t work.
Personalization starts with customer segmentation, which is the practice of grouping customers based on features like age, gender, interests, and spending habits. We do this so we can customize our marketing approaches for each customer group.

In the realm of machine learning, k-means clustering can be used to segment customers (or other data) efficiently.
K-means clustering is one of the simplest unsupervised machine learning algorithms. Here, we’ll explore what it can do and work through a simple implementation in Python.

Some facts about k-means clustering:
- K-means converges in a finite number of iterations. Since the algorithm iterates a function whose domain is a finite set, the iteration must eventually converge.
- The computational cost of the k-means algorithm is O(k*n*d), where n is the number of data points, k the number of clusters, and d the number of attributes.
- Compared to other clustering methods, the k-means clustering technique is fast and efficient in terms of its computational cost.
- It’s difficult to predict the optimal number of clusters or the value of k. To find the number of clusters, we need to run the k-means clustering algorithm for a range of k values and compare the results.

Example Implementation
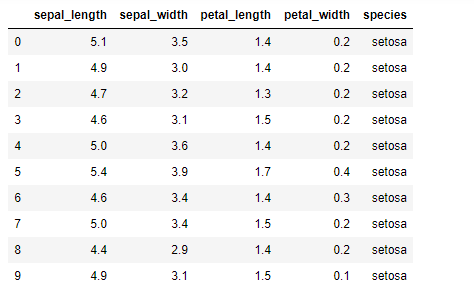
Let’s implement k-means clustering using a famous dataset: the Iris dataset. This dataset contains 3 classes of 50 instances each and each class refers to a type of iris plant. The dataset has four features: sepal length, sepal width, petal length, and petal width. The fifth column is for species, which holds the value for these types of plants. For example, one of the types is a setosa, as shown in the image below.
To start Python coding for k-means clustering, let’s start by importing the required libraries. Apart from NumPy, Pandas, and Matplotlib, we’re also importing KMeans from sklearn.cluster, as shown below.
#Import libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.cluster import KMeansWe’re reading the Iris dataset using the read_csv Pandas method and storing the data in a data frame df. After populating the data frame df, we use the head() method on the dataset to see its first 10 records.
#import the dataset
df = pd.read_csv('iris.csv')
df.head(10)Now we select all four features (sepal length, sepal width, petal length, and petal width) of the dataset in a variable called x so that we can train our model with these features. For this, we use the iloc function on df, and the column index (0,1,2,3) for the above four columns are used, as shown below:
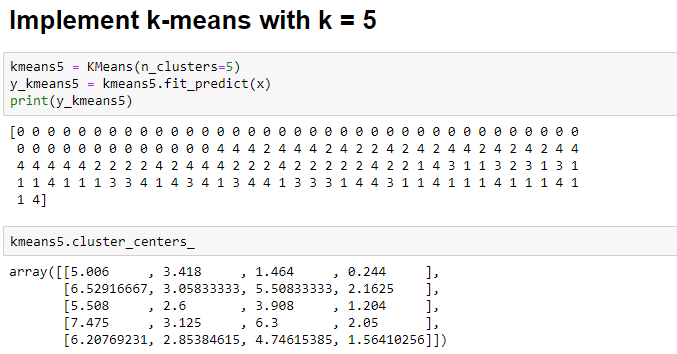
x = df.iloc[:, [0,1,2,3]].valuesTo start, let’s arbitrarily assign the value of k as 5. We will implement k-means clustering using k=5. For this we will instantiate the KMeans class and assign it to the variable kmeans5:
kmeans5 = KMeans(n_clusters=5)
y_kmeans5 = kmeans5.fit_predict(x)
print(y_kmeans5)
kmeans5.cluster_centers_Below, you can see the output of the k-means clustering model with k=5. Note that we can find the centers of 5 clusters formed from the data:
There’s a method called the Elbow method, which is designed to help find the optimal number of clusters in a dataset. So let’s use this method to calculate the optimum value of k. To implement the Elbow method, we need to create some Python code (shown below), and we’ll plot a graph between the number of clusters and the corresponding error value.
This graph generally ends up shaped like an elbow, hence its name:
Error =[]
for i in range(1, 11):
kmeans = KMeans(n_clusters = i).fit(x)
kmeans.fit(x)
Error.append(kmeans.inertia_)
import matplotlib.pyplot as plt
plt.plot(range(1, 11), Error)
plt.title('Elbow method')
plt.xlabel('No of clusters')
plt.ylabel('Error')
plt.show()The output graph of the Elbow method is shown below. Note that the shape of elbow is approximately formed at k=3.
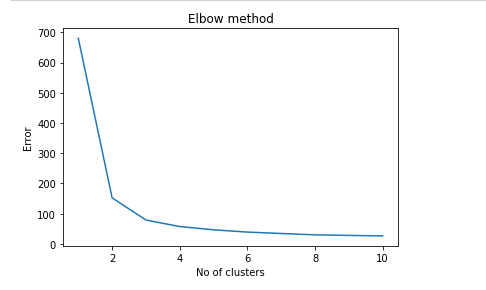
As you can see, the optimal value of k is between 2 and 4, as the elbow-like shape is formed at k=3 in the above graph.
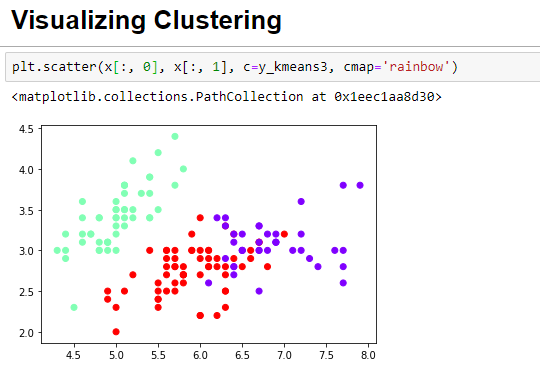
Let’s implement k-means again using k=3
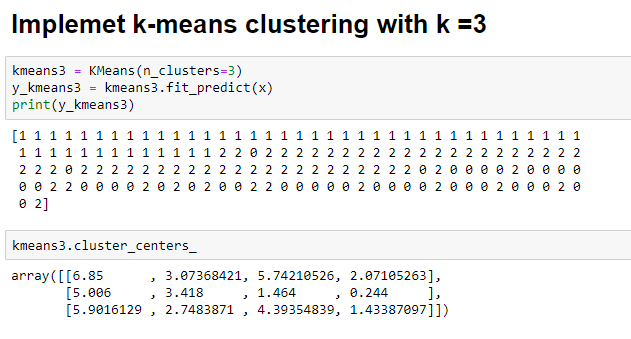
Finally, its time to visualize the three clusters that were formed with the optimal k value. You can clearly see three clusters in the image below, with each cluster represented by a different color.
Closing comments
I hope you learned how to implement k-means clustering using sklearn and Python. Finding the optimal k value is an important step here. In case the Elbow method doesn’t work, there are several other methods that can be used to find optimal value of k.
Happy Machine Learning!

Comments 0 Responses