Note: The original research report on which this post is based can be found here
Introduction
If you’re one of those people with a large number of GPU compute nodes in your basement, or if you work for Google, training neural networks in a short time for challenging tasks is probably easy for you.
However, if you don’t happen to be one of those lucky ones, you’re probably experiencing trade-offs between model size, training time, and performance. This problem is particularly pronounced on mobile and embedded systems, where computing power is very limited.
Luckily, if you have powerful processors to train on and only care about doing inference/prediction on mobile devices, there are some techniques that have you covered.
Current approaches
One way would be to start with a large network and train it using certain regularizers that encourage many weights to converge to zero over the course of training, thereby effectively pruning the network. Another way would be to train the whole network until convergence and then prune it after training, removing the connections that contribute least to the predictive performance. Ultimately, you can also train a large performant model and then distill its knowledge into a smaller model by using it as a “teacher” for the smaller “student” model.
The common thread with all these methods is that you need to start training with a large network, which requires powerful computing architecture. Once the model is trained and pruned or distilled, you can efficiently make predictions on a mobile system. But what do you do if you want to also do the training on the mobile device?
Imagine an application where you want to collect user data and build a predictive model from it, but you don’t want to transfer the data to your servers, e.g. for privacy reasons. Naïvely, one could imagine just using the pruned network architectures and training them from scratch on the device. Alas, this doesn’t work well, and it’s tricky to understand why. So how else could we tackle this problem?
The Lottery Ticket Hypothesis
It turns out that viewing pruning as identifying a sufficient model architecture could be misguided. Instead, we should perhaps view it as identifying a subnetwork that was randomly initialized with a good set of weights for the learning task. This recently published idea is called the “Lottery Ticket Hypothesis.”
The hypothesis states that, before training, randomly initializing weights will mostly assign weights that are inefficient for the task at hand. By random chance, some subnetwork will be assigned a slightly better set of weights than the other ones. This subnetwork will therefore converge quicker and will take on most of the responsibility for the actual prediction task over the course of training.
After training, it’s highly likely that this subnetwork will be responsible for most of the network’s performance, while the rest of the network might loosely support the task or be effective for some corner cases only. In line with the lottery metaphor, the authors of the paper call this special subnetwork the “winning ticket”.
Using the lottery ticket hypothesis, we can now easily explain the observation that large neural networks are more performant than small ones, but that we can still prune them after training without much of a loss in performance. A larger network just contains more different subnetworks with randomly initialized weights.
Therefore, the probability of finding a winning ticket at a certain performance level, or respectively the average performance of the network’s winning ticket, is higher. (Note that when we scale the size of all layers in a network linearly, the number of weights grows quadratically, but the number of credit assignment paths or subnetworks grows exponentially due to combinatorics!)
Empirical results
This is a compelling idea, but in order to know whether it’s actually true, the authors had to conduct a few experiments. In their first experiment, they trained the LeNet architecture on MNIST and pruned it after training up to different degrees (they call this one-shot pruning). They then reinitialized the pruned networks with the exact same weights used in the first training and retrained the so-obtained smaller networks on the same task.
They found that they can prune up to 80% of the weights while still retaining the same performance (Figure 1, left and middle). Moreover, they even achieve a faster convergence with the pruned networks. If they initialize the pruned networks with new random weights, they do not observe this effect (Figure 1, right).
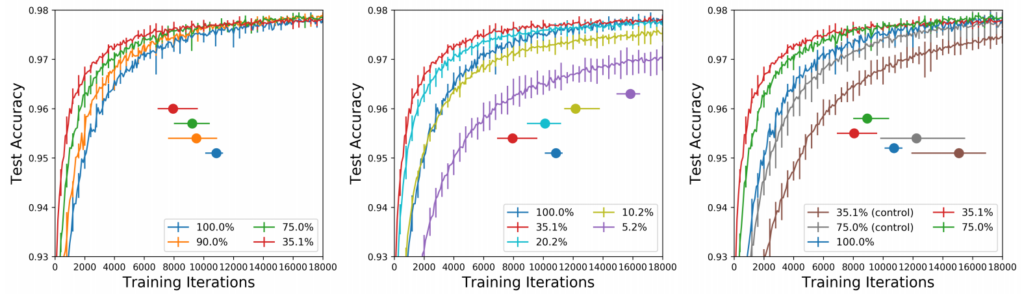
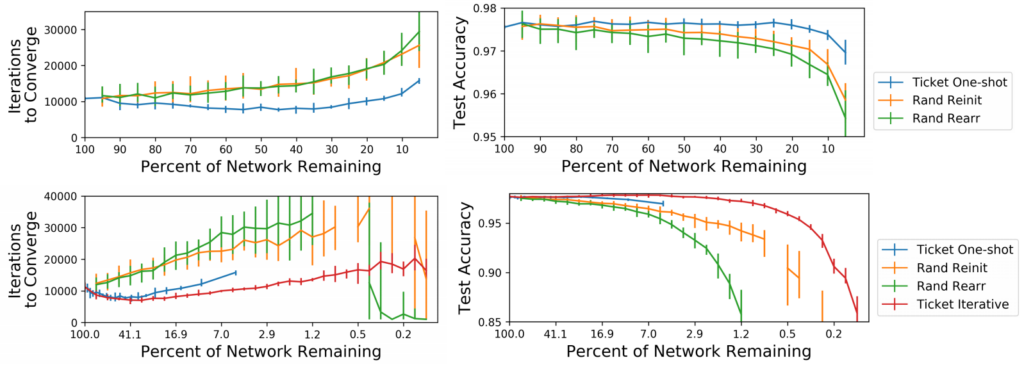
In order to test whether the structure of the pruned networks is actually also optimized for the task, as opposed to only the initial weights, the authors also compare the winning tickets to a setting where they keep the initial weights but rearrange the connections. They also try a different pruning method called iterative pruning, where they prune the networks only a little bit after training, then re-initialize and retrain and repeat that whole process a couple of times.
This is obviously more expensive than one-shot pruning, but they found it yields better results. Their results suggest that iteratively pruned winning tickets are superior to one-shot pruned ones, which are in turn superior to re-initializations of the weights and rearrangements of the connections in terms of performance and convergence speed (Figure 2).
Why does it work?
That all looks pretty neat, right? So what’s the secret of the winning tickets? What do their weights look like? It turns out that while the weights across the whole network are initialized from a Gaussian (so they have a mode at zero), the weights of the winning tickets have a bimodal distribution on the more extreme values of the initialization spectrum (Figure 3).
This effect gets stronger with the amount of pruning, i.e. the most extreme values are the last ones standing after you have pruned away all the ones closer to zero. This effect is especially pronounced in the first layers of the network.

So does this intriguing phenomenon suggest that you might want to initialize your weights from such a bimodal distribution in the first place? Sadly, the authors do not report any experiment along these lines, but I would doubt that it’s that easy. For subnetworks that are incidentally already aligned with your task objective, it makes sense that larger weights would make them even more effective.
However, there are many more subnetworks that aren’t randomly suited for your task already, and these ones would probably have a harder time learning the task if initialized with larger weights. Ultimately, the most successful strategy may well be very similar to what the authors of the paper did, namely initializing your weights from a Gaussian and then finding the optimal subnetwork with large weights that are actually helpful for your task in retrospect.
Conclusion
So what can we take away from this new research? If we want to build applications from above, where we want to train neural networks on the users’ mobile devices directly, we should first train a five to ten times larger architecture on similar data on our GPU machines.
We then can use iterative pruning to find the small winning ticket subnetwork and record its initial weight assignments. Finally, we can deploy the winning tickets with fixed weight initializations to the mobile devices and train them on the user data on-device, achieving similar performance to our larger networks but with faster convergence times.
If this all works out, we can sell our great privacy-preserving mobile neural network model and get rich without even having to win the lottery.
If you liked this story, you can follow me on Medium and Twitter.
Discuss this post on Hacker News.

Comments 0 Responses