Deep neural networks (DNNs) can have tens of thousands of parameters, and in some cases, maybe even millions. This huge number of parameters gives the network a huge amount of freedom and the flexibility to fit a high degree of complexity.
This flexibility is only good up to a certain level. When this level is crossed, the term overfitting is brought to the table.
What is Overfitting?
Overfitting happens when a machine learning model is overtrained on the training portion of the dataset, so that when the model meets new data, it performs much worse than expected.
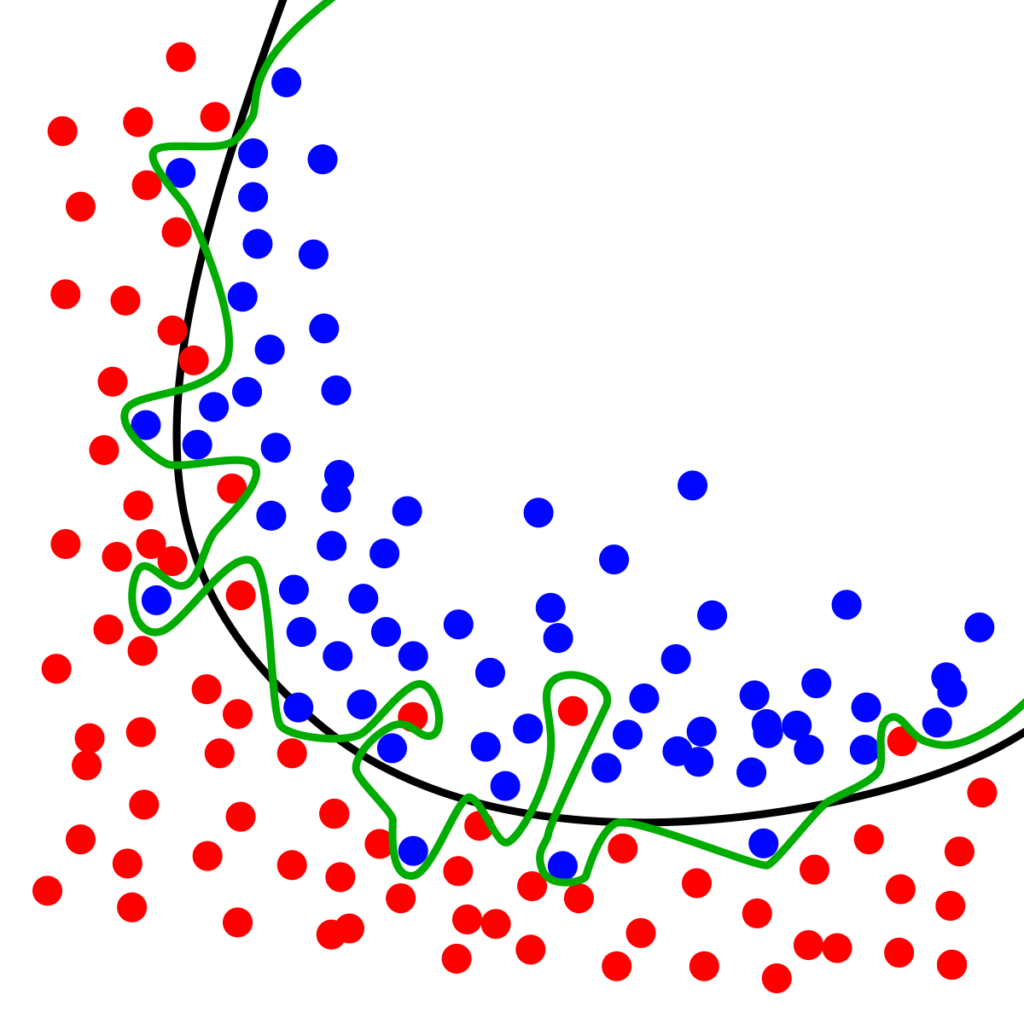
In the above figure, the green line is a perfect, too-good-to-be-true model. When such a model is evaluated on the training set, accuracy measures may reach upwards of 98% and even a solid 100%.
But this percentage gives a false impression that the model is (nearly) perfect. In reality, it’s not. Once such model is tested on unseen data, it behaves in an unexpected way. This is because it is trained so heavily on the training set that it nearly memorizes everything about the training data. The problem is, training data usually contains errors and irregularities.
There are various ways to prevent overfitting when dealing with DNNs. In this post, we’ll review these techniques and then apply them specifically to TensorFlow models:
Early Stopping
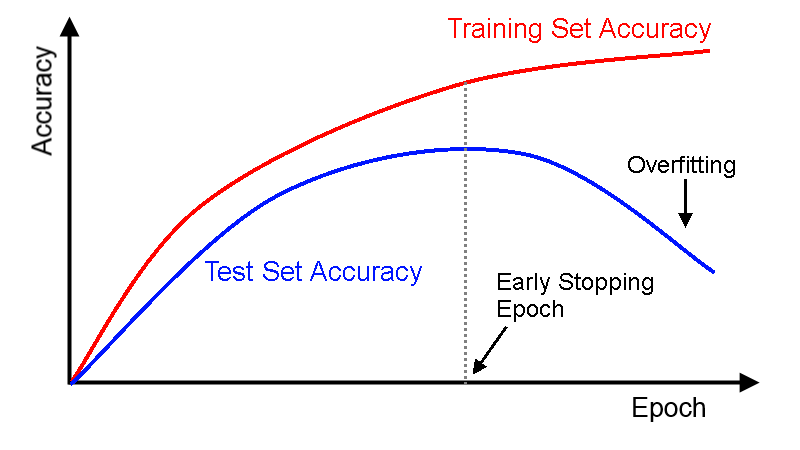
This technique refers to interrupting data when its performance on the validation set starts dropping.
With TensorFlow
- Evaluate the model on the validation set at regular intervals (e.g. 100 steps)
- Save a “best” snapshot if it outperforms the previous “best” score.
- If the interval difference since the last best exceeded a limit (e.g. 4000 steps), interrupt the training and go back to the last “best” snapshot.
Early stopping works really well in practice, but better results happen when paired with other techniques.
L1 and L2 Regularization
Regularization is a technique intended to discourage the complexity of a model by penalizing the loss function.
Regularization assumes that simpler models are better for generalization, and thus better on unseen test data. You can use L1 and L2 regularization to constrain a neural network’s connection weights.
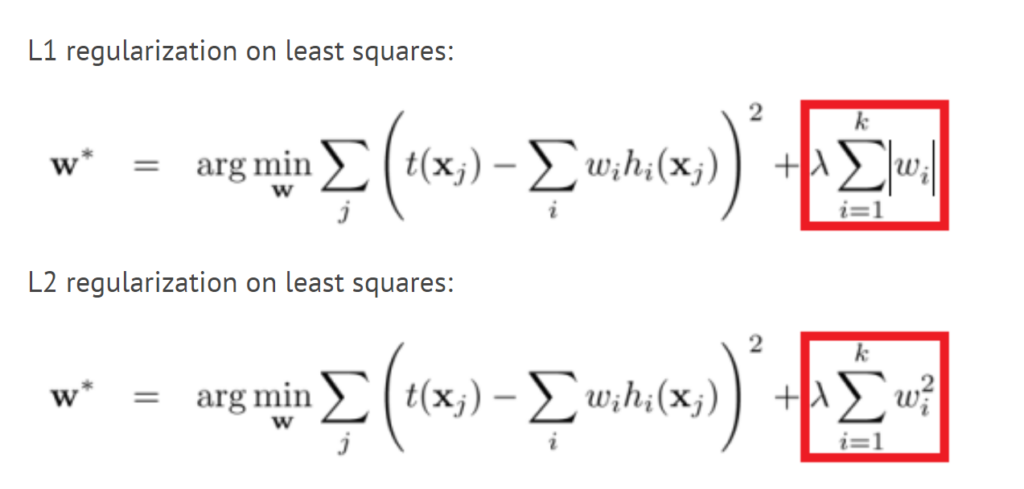
L1 is also known as the Least Absolute Deviations. It’s minimizing the sum of the absolute difference between target values and estimates (predicted) values.
L2 is known as Least Square Error. It’s minimizing the square of the sum of the difference between target values and estimates (predicted) values.
With TensorFlow
Many functions that create variables (such as get_variable() or
tf.layers.dense()) accept a *_regularizer argument for each created variable (e.g. kernel_regularizer ). You can pass any function that takes weights as an argument and returns the corresponding regularization loss. The l1_regularizer(), l2_regularizer(), and l1_l2_regularizer() functions return such functions.
This code creates a neural network with two hidden layers and one output layer, and it also creates nodes in the graph to compute the L1 regularization loss corresponding to each layer’s weights. TensorFlow automatically adds these nodes to a special collection containing all the regularization losses. You just need to add these regularization losses to your overall loss, like this:
Don’t forget to add the regularization losses to your overall loss, or else they will simply be ignored.
Dropout
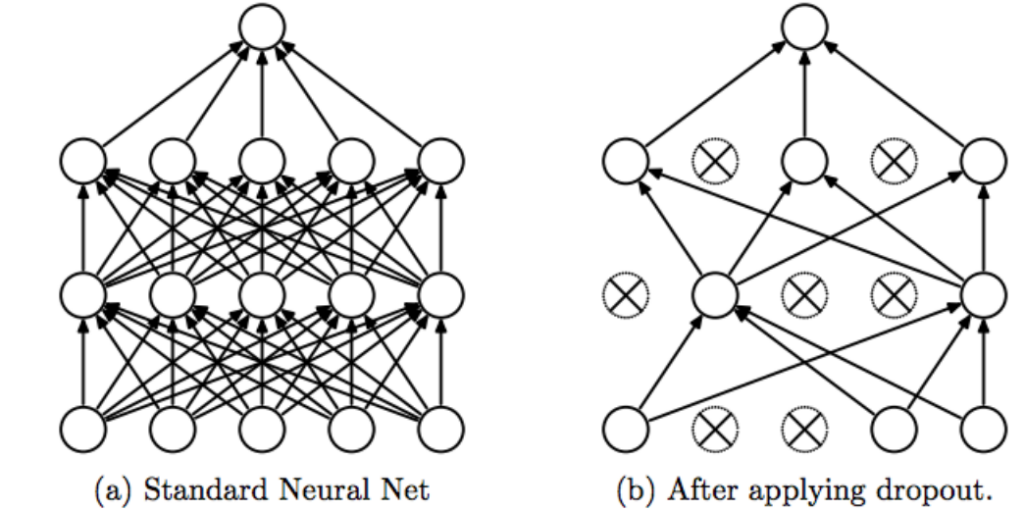
Dropout is the most common technique to combat model overfitting.
At each training step, every neuron (except the output neurons) has a probability p that it will be temporarily dropped at the current step, meaning it will be totally ignored with the possibility that it may be active the next one. The hyperparameter p is called the dropout parameter, and it’s typically set to 50%. After training, neurons aren’t dropped anymore.
With TensorFlow
You can simply apply the tf.layers.dropout() function to the
input layer and/or to the output of any hidden layer you want.
During training, the function randomly drops some items and divides the remaining by the keep probability. After training, the function does nothing.
tf.nn.dropout() is similar to tf.layers.dropout(), but it doesn’t turn off the dropout when not training, which is usually not what we want.
Max-Norm Regularization

For each neuron, max-norm regularization constrains the w of incoming connections such that w ≤ r, where r is the max-norm hyperparameter. We do this by computing w after each training step and clipping w if needed.
With TensorFlow
TensorFlow doesn’t offer an off-the-shelf max-norm regularizer, but it’s easy to implement one.
- Get the handle on the weights of the first hidden layer.
- Use clip_by_norm() to create an operation that weights along the second axis so that each row vector ends up with a maximum norm of 1.0.
- The last line creates an assignment operation that will assign the clipped weights to the weights variable.
Then you just apply this operation after each training step.
You do the above for every hidden layer you’ve got.
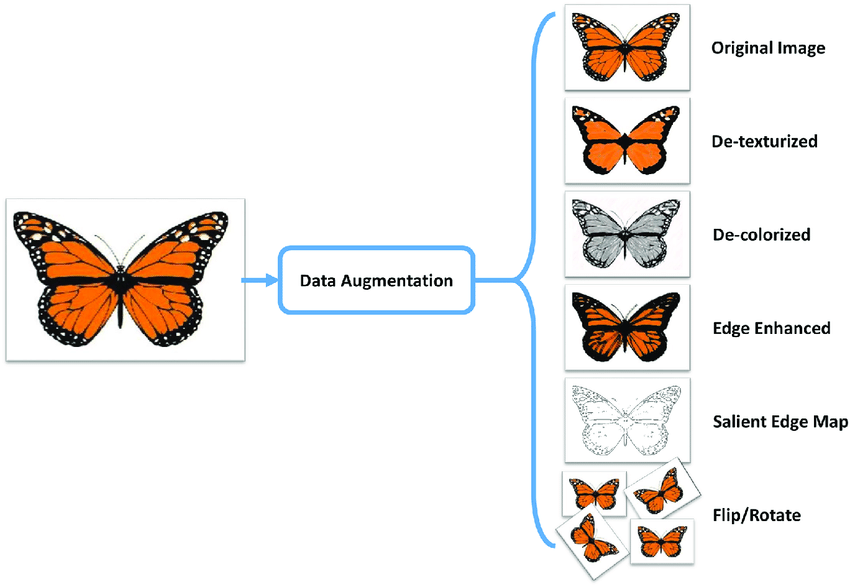
Data Augmentation
Another way to eliminate overfitting is data augmentation. Data augmentation is the artificial reproduction of new training instances out of existing ones. This boosts the training set size.
The trick is to generate realistic training instances such that a human can’t tell the difference between original ones and the ones you’ve created.
For example, if you’re working on classifying dog breeds, you can simply rotate, shift, and resize every image you have by various amounts and add the resulting images in the training set. Also, you could flip or increase/decrease contrast in each photo.
There are other filters that you could apply such as de-texturizing, de-colorizing, edge enhancement, salient edge mapping, and more.
With TensorFlow
No special technique needed for data augmentation with TensorFlow. Just basic image processing tools such as OpenCV.
OpenCV comes in very handy in image processing, here’s a quick read about it.
This has ready-made code snippets of every manipulation technique you’ll need to data-augment your data set,
A lot of the info I wrote here came from the book Hands-On Machine Learning with Scikit-Learn &TensorFlow, which I highly recommend.

Lastly, here’s a paper titled “Dropout: A Simple Way to Prevent Neural Networks from Overfitting” that proved on the MNIST dataset that dropout + max-norm regularization gave the least error score i.e. best results.

Comments 0 Responses