📱 Mobile Machine Learning
Genetic Algorithms (GAs) are a subset of Evolutionary Algorithms, which use mechanisms inspired by nature such as mutation, evolution, reproduction, etc. In spite of using advanced math, these algorithms work on principles which are derived from nature. Growth of an organism in its environment and its interaction with other beings in that environment can be modeled with simple mathematical expressions.
Today, we’ll perform Hyperparameter Optimization with GAs to see how neural networks can be treated as individuals living in a population where each one has its own set of genes (which are actually hyperparameters).
Hyperparameter optimizations consist of those techniques through which we can determine the best combination of hyperparameters (constant parameters which are to be given to the model) so as to have the best results from the model. A “best combination” would mean a set of hyperparameters which give the least value for our loss function in one single iteration. With the help of GAs, we’ll evolve various sets of hyperparameters using Charles Darwin’s principle of Natural Selection. It’s quite famous in biology textbooks, but essentially deems that the ability to evolve is what carries on from generation to generation and that traits will be selected for their usefulness.

Prerequisites
You need not be an AI researcher to understand this, but make sure that you know how we implement Feedforward Neural Networks in Kotlin as I’ll be omitting that code in the later sections. Read it here:
Basically we’ll be doing two things: We’ll optimize only three hyperparameters and we’ll train our model only on one sample and thereby calculate the loss.
Starting with Layman definitions
We’ll first have a short description of what GAs and hyperparameters are. You may visit Wikipedia for Genetic Algorithms and Hyperparameter Optimization for more detailed explanations.
Genetic Algorithms: GAs are algorithms inspired by Charles Darwin’s Theory of Natural Selection. It works on the principle of natural selection, where the fittest individuals are selected from a population, to produce offspring who form the next generation of the population with the best adaptations.
Hyperparameter Optimization: In machine learning, hyperparameter optimization, or tuning, is the problem of choosing a set of optimal hyperparameters for a learning algorithm.
We’ll now try to learn some biological terms which will help us in creating a crystal-clear image of what a GA actually does.
Getting into the Biology …
Below are each of the elements required in GAs. By understanding the analogy, we’ll get a clearer intuition on the functioning of GAs.
1. Genes and Chromosome
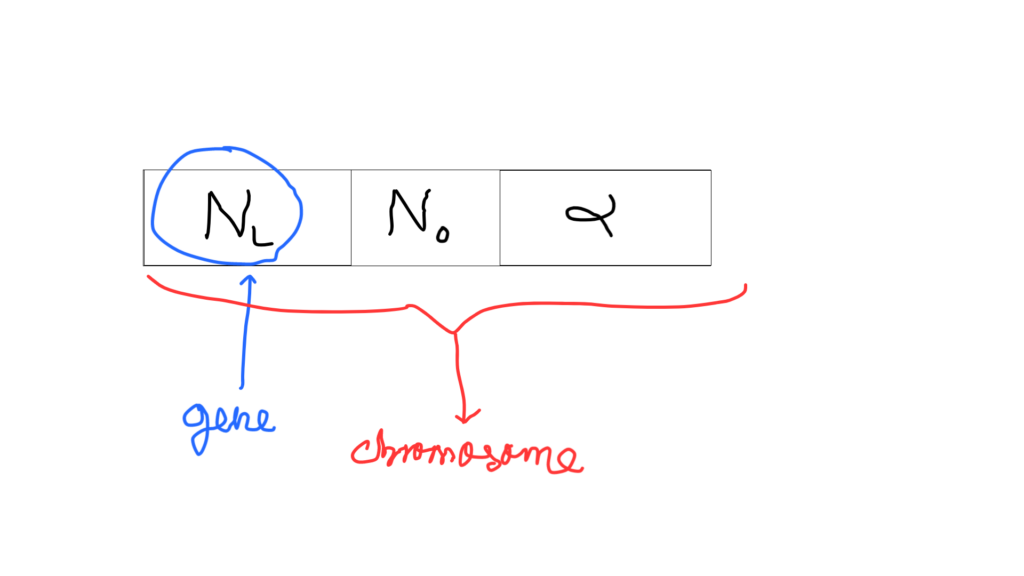
Genes or Genetics are the building blocks of every form of life on Earth. Basically, a gene describes the synthesis of a certain compound which is necessary for life. In our case, we would treat a “gene” as a hyperparameter.
A gene is contained in a chromosome, which could be considered as a set of hyperparameters for a NN. A Neural Network will be an individual with certain genes (hyperparameters). In the image above, we can see three genes/hyperparameters, which we’ll discuss later.
2. Population
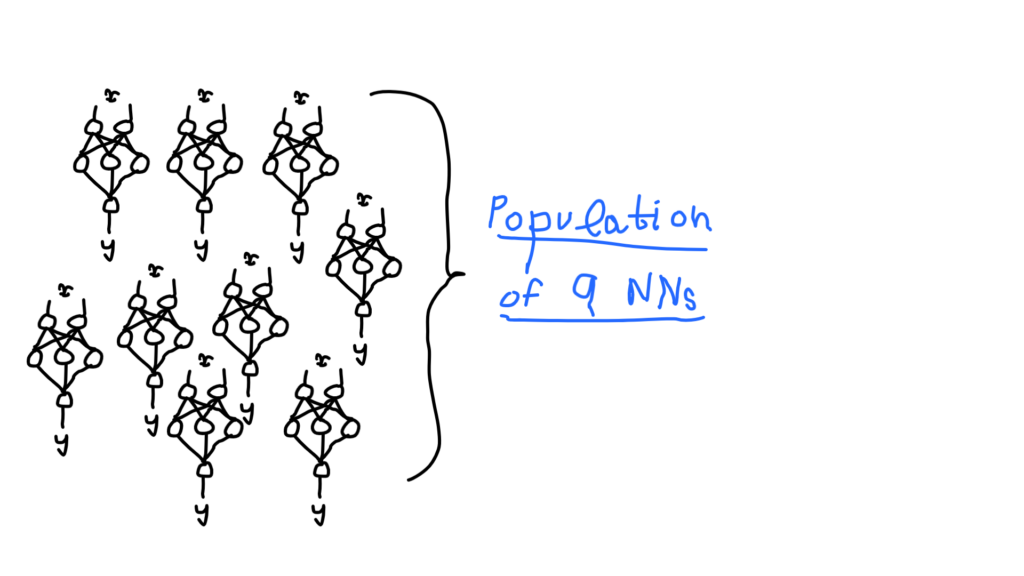
A population is a group of certain individuals who possess similarities in their structure or functioning. As in the picture above, we can see a population consisting of nine neural networks. We’ll be selecting the fittest neural networks from this population. Evolution of individuals would also occur within a population only.
3. Breeding
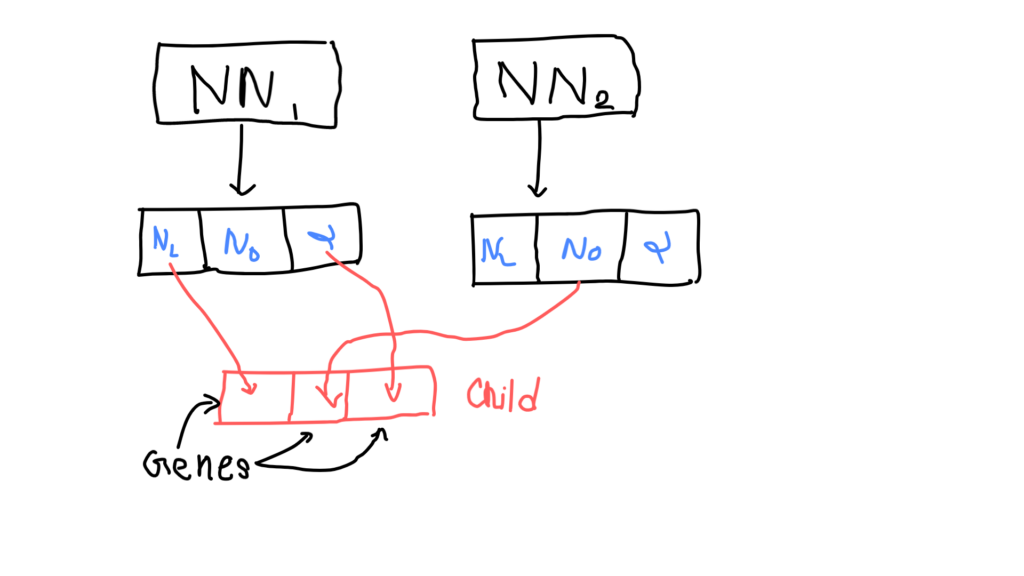
Producing individuals from existing members, where both contribute equal genetic material, is called breeding. Here, we’ll take two NNs and produce two new NNs (offspring) who will have the same genetics from both their parents. Meaning, the two newly produced NNs will share the same values for hyperparameters which their parents did.
4. Mutation
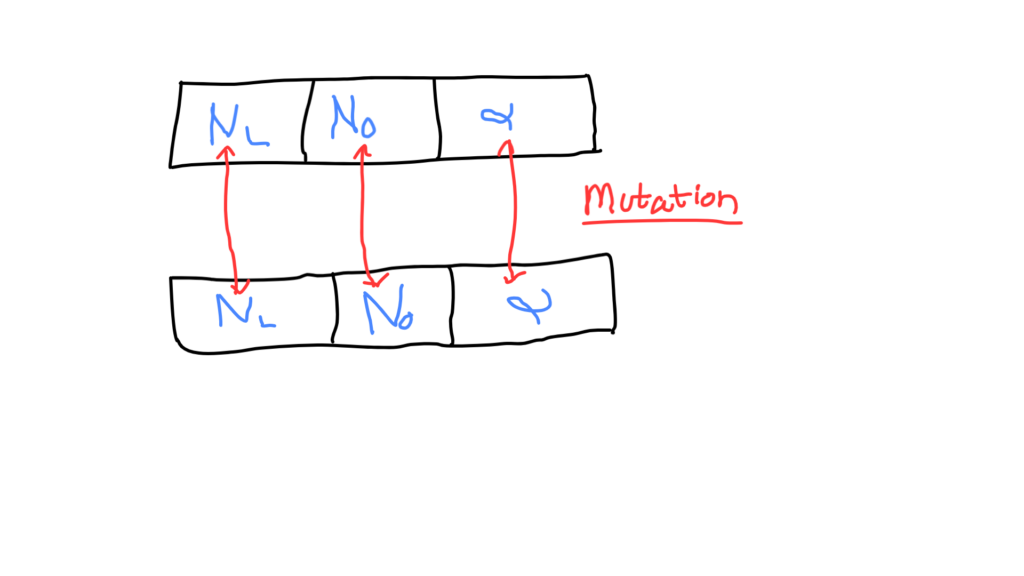
If we’re copying the whole genetic sequence of the parents to their offspring, there will be no diversity in the population. Everyone will have the same characteristics and hence no competition for survival.
In order to maintain diversity or stochasticity, we randomly mutate the genes of the children. So, in our case, we’ll randomly modify the genes (values of hyperparameters) of the children with some probability (which we’ll discuss in later sections).
5. Fitness Score
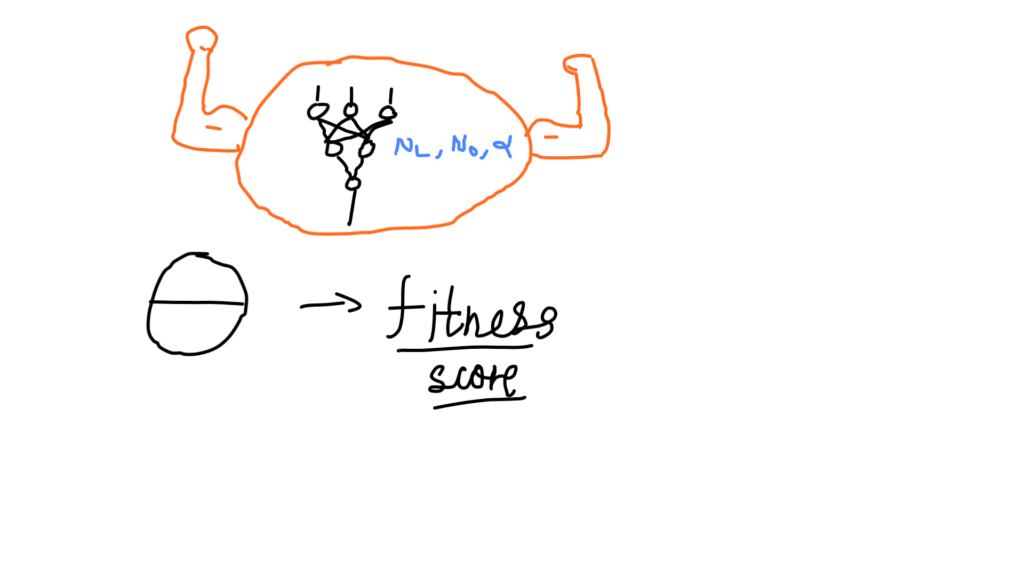
Fitness score isn’t a biological term but we’ll have to use it to determine the strongest neural network in our population. The NN which will have the lowest value for the loss function will be termed as the fittest. We’ll represent the fitness score as θ.
In nature, we have various aspects to determine the survival of a being, like physical power and size. But for our NNs, we’ll have a fitness score which would also decide their chances of being evolved.
Surprise! Math is here!
We’ll first require a Neural Network whose hyperparameters can be optimized. I’ve explained how we can construct feed-forward neural networks in Kotlin in this story:
We need to determine three hyperparameters for our model, using Genetic Algorithms. They are the number of layers (dense layers), neurons in each layer and the learning rate.
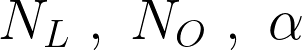
In the context of GAs, these three hyperparameters will act as genes for an individual. By an “individual,” we mean a Neural Network with a given set of genes (hyperparameters as seen as in the image above). We won’t use any real number for these three hyperparameters. Our NN will have choices, as shown below.

We’ll represent our model with F, which takes in the above-mentioned hyperparameters as well as input x (sample) and produces an output. With less vigorous notation, this idea can be expressed as:
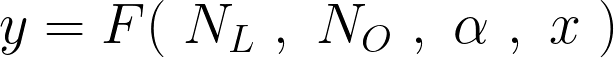
Next, we’ll require a fitness score to choose which individuals will be evolved into the next generation. Remember Charles Darwin’s principle, survival of the fittest? In order to determine the top N fittest members in a population, we’ll use this fitness score.
Among the NNs (i.e in the population of NNs), the NN which has the least value for the loss function, will be the fittest. So, in general, the fitness score should vary inversely with the value of the loss function for a given set of hyperparameters (genes).
We’ll have a super simple loss function:
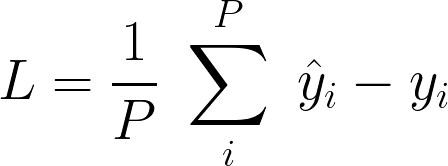
Using the loss function, we define a fitness score, for our model,
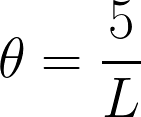
After getting a concrete understanding of the variables a GA would use, we’ll head towards the Kotlin implementation of the GA.
Getting into the code …
Make sure you’ve opened up the GitHub repo in another tab. I’ll refer to various classes which are present there.
We’ll now create the Train class in Kotlin. This class will create a Model with the given hyperparameters and train a NN with them. On calling the trainAndScore() method, a forward pass will be performed and we’ll get the fitness score for the hyperparameters provided to it.
import NeuralNetwork.ActivationOps
import NeuralNetwork.Dense
import NeuralNetwork.MatrixOps
import NeuralNetwork.Model
// The class which trains the NN and stores the fitness score.
class Train {
// NN Model
private lateinit var model : Model
// Inputs given to the NN
private val inputs = MatrixOps.uniform( 1 , 3 )
// Labels for the given input
private val outputs = MatrixOps.uniform( 1 , 2 )
// Number of iterations to train for
private val numIterations : Int = 1
// Input/Output dimensions
private val inputDims : Int = 3
private var outputDims : Int = 2
// Compile the model with given hyperparameters.
private fun compileModel( networkParams : HashMap<String,Float> ) {
val numLayers = networkParams[ "numLayers" ]!!
val numNeurons = networkParams[ "numNeurons" ]!!
val learningRate = networkParams[ "learningRates" ]!!
// Add required number layers and neurons in each
val layers = ArrayList<Dense>()
for ( i in 0 until numLayers.toInt() ) {
layers.add( Dense( numNeurons.toInt() , ActivationOps.ReLU() , false ) )
}
layers.add( Dense( outputDims , ActivationOps.ReLU() , false ) )
model = Model( inputDims , layers.toTypedArray() , learningRate.toDouble() )
model.compile()
}
// Train a member ( neural network ) for a given number of epochs.
// Return the fitness score which is ( 5 / loss )
fun trainAndScore( networkParams : HashMap<String,Float> ) : Float {
compileModel( networkParams )
for (i in 0 until numIterations ) {
println( "Training this individual for ${i+1} epochs")
model.forward(inputs, outputs)
model.backward()
}
val loss = MatrixOps.sum_along_axis0(outputs - model.forward(inputs, outputs)) / outputDims
return ( 5.0 / loss).toFloat()
}
}Also, have a look at the Network.kt file.
Next, we’ll require a helper class Optimizer which will help us create a new population, perform mutation between two individuals, and also evolve them. There are several methods in this class, so we’ll take them one-by-one to have a clear glimpse of what’s going on inside.
// Class which uses the Genetic algorithm for optimization.
class Optimizer(
private var paramChoices : HashMap<String,FloatArray> ,
private var mutateProb : Float = 0.2f ,
private var randomSelect : Float = 0.3f ,
private var retain : Float = 0.3f
) {
// Other methods here
}- The paramChoices hashmap holds various choices for our three hyperparameters. So, we need to pick the best combination of these choices only.
- The mutateProb denotes the probability of a child getting mutated. It is used in the breed() method, which we’ll discuss later.
- The randomSelect denotes the probability of a parent being selected for breeding. It is used in the evolve() method.
- The retain value denotes the number of individuals selected for breeding. The top K members will be selected who have the highest value for the fitness function. Here, K = population.size * retain. It is used in the evolve() method.
To start the process of hyperparameter optimization, we’ll first require some individuals, right? We’ll need an initial population from where we can select the fittest and then breed them with each other. In other words, we’ll need a set of NNs (initialized with random weights, biases and the three hyperparameters) stored in a ArrayList.
// Create an initial population from where the optimization can start, given the no. of
// members/individuals required.
fun createPopulation( numIndividuals : Int ) : ArrayList<Network> {
val population = ArrayList<Network>()
// Add each member
for (i in 0 until numIndividuals) {
val individual = Network()
// Each member will have the same set of choices
individual.paramChoices = paramChoices
// Initialize this member with random picked choices
individual.initializeNNWithRandomParams()
population.add( individual )
}
return population
}Wondering what individual.initializeNNWithRandomParams() does? See the Network.kt class.
We’ll now write a method which can breed two Neural Networks, i.e., produce two children from two parents. Meaning, we will pick up genes randomly from the mother and the father and add them in the children. We’ll keep this choice random, so as to have diversity in our population. It’s obvious that children inherit characteristics from both their parents.
// Produce two children from their parents
private fun breed( mother : Network , father : Network ) : ArrayList<Network> {
val children = ArrayList<Network>()
for( i in 0 until 2 ) {
// Create parameters for the child NN
val childParams = HashMap<String,Float>()
for ( param in paramChoices.keys ){
childParams[ param ] = arrayOf(
mother.networkParams[ param ] , father.networkParams[ param ] ).random() as Float
}
var child = Network()
child.networkParams = childParams
// Perform mutation
if ( mutateProb > Random().nextFloat() ) {
child = mutate( child )
}
children.add( child )
}
return children
}childParams[ param ] is picked randomly from { mother.networkParams[ param ] , father.networkParams[ param ] }. We now have to explore the mutate function, which, as the name suggests, is a performed mutation of genes.
// Mutate the parameters of the child NN
private fun mutate( child : Network ) : Network {
// Choose any random parameter which will be mutated
val randomParam = paramChoices.keys.random()
// Choose any random value for that parameter ( chosen above )
child.networkParams[ randomParam ] = paramChoices[ randomParam ]!!.random()
return child
}In our case, mutation means to swap a gene (one of the three hyperparameters) with any of the possible values available for that gene, as shown in Snippet 1.
Now its time to encapsulate all our methods in the evolve() method. It will perform the following operations given the currentPopulation.
- Sort the members according to their fitness score with the sortedWith() method. The ones with the highest fitness score, i.e., the NNs with the lowest value for the loss function (remember the fitness score varies inversely with the loss) are at the beginning of the list (ascending order of the fitness score).
- The top K individuals with the highest fitness scores are added in a separate ArrayList called parents. Here ‘K’ is the retainLength as seen in the snippet below.
- Apart from these, we randomly add some other individuals, which have lower fitness scores below our desired threshold. This increases diversity as we are introducing some ‘weaker’ parent NNs into the next generation too.
- Select two individuals randomly from parents and check that they are not the same. Call breed() on them and append the babies (output of the breed() method) to children.
- Append the children to the parents array.
fun evolve( currentPopulation : ArrayList<Network> ) : ArrayList<Network> {
// Get the fitness scores of all individuals in this population and sort them.
val populationSorted = currentPopulation.sortedWith( kotlin.Comparator {
o1, o2 -> o2.score.compareTo( o1.score ) })
// Select top K individuals ( which have the highest fitness score ) from this population
val retainLength = ( currentPopulation.size * retain ).toInt()
val parents = ArrayList( populationSorted.slice( 0..retainLength ) )
// Add some more individuals ( the ones filtered above )
for ( unwantedParent in currentPopulation.subList( retainLength , currentPopulation.size ) ) {
if ( randomSelect > Random().nextFloat() ) {
parents.add( unwantedParent )
}
}
// Create an array ( of length (total_individuals - selected_parents) ) to store children.
val parentsLength = parents.size
val desiredLength = currentPopulation.size - parentsLength
val children = ArrayList<Network>()
while( children.size < desiredLength ) {
// Select any two parents
val male = Random().nextInt( parents.size )
val female = Random().nextInt( parents.size )
// Check if they are different from each other
if ( male != female ){
val maleParent = parents[ male ]
val femaleParent = parents[ female ]
// Perform breeding
val babies = breed( maleParent , femaleParent )
// Append the babies to the arraylist
for ( baby in babies ){
children.add( baby )
println( "Adding children")
}
}
}
parents.addAll( children )
return parents
}We’ve completed writing all the methods required for our GA. We’ll now head towards running the GA.
Time for some evolution!
Now that we have implemented all the required methods in the Optimizer class, we’re ready to run our GA.
fun main() {
// Number of generations to be evolved
val numGenerations = 10
// Number of individuals in each population. In our case, this is the number of networks
// which will be trained for 1 iteration so as to get the loss incurred by each NN.
val population = 20
val paramChoices = HashMap<String,FloatArray>()
paramChoices[ "numLayers" ] = floatArrayOf( 2f , 3f , 4f )
paramChoices[ "numNeurons" ] = floatArrayOf( 12f , 10f , 8f )
paramChoices[ "learningRates" ] = floatArrayOf( 0.01f , 0.001f , 0.005f )
// Create an optimizer.
val optimizer = Optimizer( paramChoices )
// Create a population with NNs consisting of randomly chosen parameters.
var individuals = optimizer.createPopulation( population )
for ( i in 0 until numGenerations ){
for ( individual in individuals ){
individual.train()
}
val avgScore = optimizer.getAvgScore( individuals )
if ( i != numGenerations - 1 ){
individuals = optimizer.evolve( individuals )
}
}
}- numGenerations defines the number of times the evolution would occur. After every evolution, a new population will be born.
- population is the number of individuals present in the population. More members will lead to greater diversity.
- Next, we call optimizer.createPopulation which returns a ArrayList<Network> representing each individual. The genes (i.e the three hyperparameters) are randomly set in these individuals, as we’ve seen before.
- In the for{ } loop, we’ll first call train() on every individual so as to get the fitness score of that individual. Note, that the fitness score varies inversely with the loss function.
- Finally, we’ll call optimizer.evolve() to evolve the current population.
We’ll also add some code, to print the NN with the highest fitness score.

The output of this code (this might change when you run the code).

After hyperparameter optimization, we’ve got these parameters which would yield the lowest value for our loss function.
That’s All! You’ve just created a Genetic Algorithm in Kotlin!
We can include more hyperparameters for optimization. Also, we can use a different strategy for calculating the fitness score. Here, we’ve directly used the value of the loss function, but a detailed expression could also be employed.
We can use more samples, for calculating the fitness score. Try playing with the numGenerations and population variables. Train the model for more number of epochs, but this would increase the computational time for the GA.
To read more stories on Mobile Machine Learning and ML in Kotlin, please consider visiting my Medium profile. Thanks for reading!

Comments 0 Responses