Demystifying Capsule Networks

Deep learning has taken the world by a storm in recent years. From self-driving cars to predictive advertising, it has inevitably become a major part of our day-to-day lives.

Geoffrey Hinton, the person credited to bringing deep learning back into the mainstream and largely responsible for what it is today, released an entirely new type of neural network known as the Capsule Network (or CapsNet). As the name suggests, it uses capsules rather than artificial neurons for its activities.

Hinton, Sabour and Frosst described the intuition and the workings of the proposed network in their paper Dynamic Routing Between Capsules, published in 2017. They also expounded upon an approach in their paper which claimed to reduce error rates on the MNIST dataset. The results were claimed to be considerably better than a conventional CNN on highly overlapped digits.

This article tries to give the reader a broad overview (while covering the finer points) into the genius of Hinton and his team, and why the CapsNet is a network to be reckoned with.

But what are Capsule Networks?

Capsule networks (or CapsNets) are the brainchild of Geoffrey Hinton and his research team. Released in 2017, it can be described as a machine learning approach as an attempt to more closely mimic biological neural organization using artificial neural networks.

When the paper describing capsule networks was initially released, it caused a lot of excitement within the deep learning community. This was mainly because the paper introduced an entirely new concept, something that did not follow the traditional layered structure of neural networks, but approached the problem in an entirely way. The idea described in the paper released by Hinton and his team was to add structures called capsules to a conventional CNN and to reuse the output from several of these capsules to form more stable representations for higher capsules in the network.

What are capsules and why do they work?

A capsule can be defined as a set of neurons that individually activate for various attributes of an object such as position, hue and size. The probability of the entity’s presence in a specific input can be defined as the length of the vector that is derived from the output of the capsule, while the vector’s orientation is used to quantify the capsule’s properties.

Unlike artificial neurons, capsules are independent in nature. This means that, when multiple capsules agree with each other, the probability of a correct detection is much higher.

So now that we know what CapsNets are made up of, we need to better understand how they work—or to put it more accurately, how do capsules compare to artificial neurons?

To answer these questions, we can refer to Hinton’s first paper where he introduced capsules.

Capsules are an alternative to artificial neural layers, through which one is able to store all necessary and required information about the state of the features in the form of a vector. According to Hinton and his team, each capsule performs quite complicated internal computations on its input and then encapsulates the result into a small vector of highly informative output. This is much better compared to artificial neurons that use a single scalar output to show the final results of the computations.

Let’s illustrate this with the help of an example. Let’s say we’re working with a convolutional neural network (CNN), which is used at the forefront of nearly every computer-vision based application in today’s world.

CNNs work by using a convolutional layer that divides the given input into sectors. These layers then replicate each sector’s weight to give a 2-dimensional matrix, which is stacked over to get the output of the convolutional layer. After that, we use a max pooling layer that looks at each of the regions in the 2-dimensional matrix, and selects the largest number in each region (a scalar quantity). As a result, when we change the positioning of the object by a little bit, the outputs of the neurons of the networks remain the same.

The described mechanism does work extremely well in practice, but it tends to have some flaws, mainly because of the max pooling part of the architecture. Max pooling tends to lose valuable information provided by the convolutional layer, and it’s also unable to encode spatial relationships between features.

Capsules, on the other hand, tend to encode the probability of required feature detection as the length of their output vector. Being a vector, the output also has a directional component, which is used in the encoding of the state of the detected feature. In this case, when the positioning of the object from which the features are to be detected is changed, the probability of the detection (represented by the magnitude of the vector) remains the same, but the orientation does change with the change in the positioning of the object.

If the above seems too theoretical and confusing, the next section will hopefully help you understand what exactly the drawbacks of CNNs are.

Why Not Convolutional Neural Networks?

Convolutional neural networks (CNNs) have been around for a long of time. In fact, they are one of the main reasons why deep learning is so popular today. CNNs are usually attributed with giving machines the power to decipher and analyze images. However, as is the point of this article, CNNs also tend to have certain limitations.

The main feature of a CNN is its convolutional layer. It detects important features of an image in its pixels. The deeper layers present in the network would tend to detect simpler features (like edges and contours) compared to higher layers which would combine these simpler features to detect more complex features and eventually produce classification predictions.

Max Pechyonkin gives a great example in his blog that captures the major drawback of conventional CNNs. It mainly summarizes the fact that CNNs do not usually take spatial distances between features into account while predicting features and classifying images.

The example that Max took was of a digitally edited image, where the components were that of a face (eyes, nose, mouth) were jumbled together. For a CNN, the very presence of these parts is strong evidence that there is a face present in the image. It wouldn’t matter whether the mouth is above the eyes or below. Since the higher layers would detect the features relevant to the faces that they were trained on, they would detect faces.

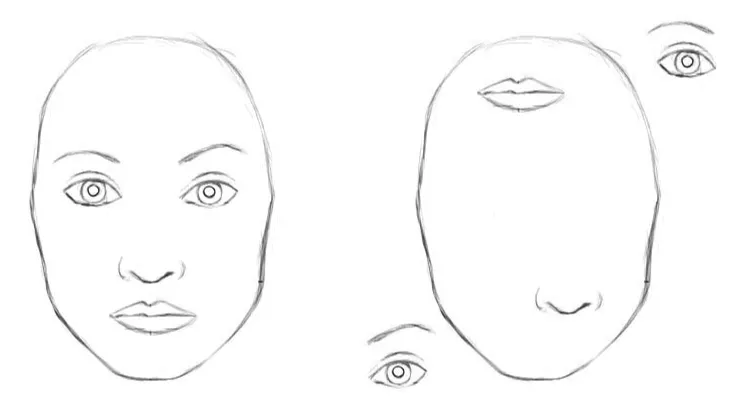
The reason for this problem? Max pooling. Max pooling, while on one hand a method that makes CNNs work surprisingly well, is also responsible for the loss of invaluable information like the pose relationship between the higher-level features.

In short, the layers in a CNN do not take into account the important spatial hierarchies between the detected features of an image. Taking the example above, the mere presence of eyes and mouth should not be enough to detect a face. The neural network should also be able to discern if and how these features are oriented with respect to each other.

Capsule Network Architecture

Here, I’ll describe the capsule network architecture in a short and succinct manner.

The capsule network that was defined by the authors in the paper can be divided into two main parts: Encoder and Decoder

CapsNet Encoder

The encoder has 3 main layers associated with it. They are summarized as follows:

1. Convolutional Layer: This layer’s job is to detect basic features in a two-dimensional image. In CapsNet, the convolutional layer has 256 kernels of size 9x9x1 and a stride of 1.
2. PrimaryCaps Layer: This layer has the primary capsules (which give the network its name) whose job is to take the outputs of features that are detected by the convolutional layer and produce combinations of the input features. The layer has 32 ‘primary capsules’, and each capsule produces an output tensor of shape 6x6x8. The final output of this layer has a shape of 6x6x8x32 (since there are 32 capsules).
3. DigitCaps Layer: This layer has 10 capsules, one for each digit. (Note: This is specific to this network, since the network was trained on the MNIST dataset, which needs to produce an output probability for 10 classes). Each capsule takes in a 6x6x8x32 shape vector and outputs a 16×10 matrix; which goes to the decoder.

CapsNet Decoder

The CapsNet decoder has 3 fully-connected layers (FCs) that take in a 16-dimensional input from the DigitCaps layer and learns to decode it into an image. The size of the image that is recreated in the paper is 28×28 pixels.

The Dynamic Routing Algorithm

Any blog that talks about capsule networks has to mention the dynamic routing algorithm. It’s a novel algorithm used to train a capsule network to make it perform the way it does.

To anybody that wants to dig into the nitty-gritty of the algorithm, I’d highly recommended reading the original paper that introduced it to the world. However, not all of us have the heart to read through technical jargon and long papers. The below section gives a broad overview of this algorithm.

The Intuition

The main intuition behind the algorithm can be best described as it’s given in the paper:

Since the output of a capsule is a vector, it makes it possible to use a powerful dynamic routing mechanism to ensure that the output of each capsule gets sent to a specific and appropriate parent in the layer above it.

The algorithm has some similarity to traditional training methods in the sense that the higher-level capsules cover larger regions of the image. However, it disregards the max pooling step, which as a reminder is associated with training of CNNs. Dynamic routing does not dispose of information about the precise position of the entity within the region.

For capsules that are present in the lower level of the hierarchy, the location information is place-coded depending upon which capsule is active at a given moment. As we move up the network, more and more information starts to get rate-coded in the magnitude component of the capsule’s output vector.

Now that we have a basic idea of the algorithms basic intuition, we can further examine the dynamic routing algorithm in a step-wise manner.

The Algorithm

Here’s an excerpt from the paper that describes the algorithm line-by-line, followed by a summary of what the algorithm actually does:

Before we see what exactly’s happening in the algorithm, we need to know what exactly needs to be achieved. A capsule i in a lower-level layer needs to decide how to send its output vector to higher-level capsules j. It makes the decision by changing the scalar weight c[ij], which will multiply its output vector and then be treated as input to a capsule above in the hierarchy.

1. The first line of the procedure takes all present capsules at a lower level l and their outputs u, as well as the number of routing iterations r that are given by the user. The last line suggests that the procedure would produce the output of a capsule present above in the hierarchy of the network, v[j]. To those familiar with training of neural networks, this algorithm can be considered somewhat analogous to the forward pass of a conventional neural network.
2. The second line defines a coefficient b[ij] which is a temporary value that is iteratively updated and stored in c[ij] after the procedure is over. It’s initialized as 0 at the start of the procedure.
3. The third line signifies that the lines 4–7 would be iteratively repeated for r times.
4. The fourth line calculates the value of the vector c[i], which are all the weights for the lower-level capsule i. This process is then done for all lower level capsules. Softmax is used to ensure that each weight c[ij] that’s captured is non-negative, and that the sum of all weights eventually is equal to one.
5. After the weights are calculated for all lower level capsules, step five calculates a linearly related combination of all obtained input vectors. Each input vector is weighted by the routing coefficient c[ij] that was determined in the previous step.
6. The sixth line describes the vectors being passed through the squash non-linearity, which ensures the preservation of the direction component of the vector, but its length is enforced to be no more than one.

Suggestions from the authors

The paper examines a range of values for both the MNIST as well as the CIFAR datasets. There are two main suggestions given by the authors in the paper that can be important to note while training a capsule network: More iterations tend to overfit the data and it’s recommended to use 3 routing iterations in practice.

The Code

For those of us that need to see the results with our own eyes, the official models that were used in the paper for the dynamic routing algorithm have been released by the authors. You can find them here:

Applications and Implementations

The best measure of any idea can be taken from practical examples and works that have been done based on it. As mentioned before, capsule networks took the deep learning community by storm when released, and since then, there have been a number of works that have been published with a capsule network at its foundation.

Capsule nets have now been proposed to be used in a variety of areas, from sentiment analysis to object segmentation to lung cancer screening.

Limitations

Even though capsule networks open up a whole new range of possibilities, they still have not been able to surpass convolutional neural networks in most fields, despite having better accuracy when compared to the former.

While capsule networks do tend to solve the core issues faced by convolutional neural networks, they still have a long way to go. Capsule networks have not been tested satisfactorily on large datasets like ImageNet, which has lead to some doubt about its ability to perform well (better than existing approaches) on large datasets.

Also, CapsNets are tediously slow to train and validate. This is because of the inner loop of the dynamic routing algorithm. This renders it incompatible for efficient training on fairly large datasets, as the number of iterations that would be required would be quite a lot. In addition, it also remains to be seen how well capsule networks work on more complex datasets and in different domains.

Conclusion

Hinton and his team introduced the world to a new building block—capsules—that has the potential to be used in deep learning to better model spatial and hierarchical relationships between internal representations of knowledge within a neural network. The intuition behind them is cunningly simple and yet has elegance to it.

With the amount of research going into capsule networks, it’s only a matter of time until it further expands into other domains of deep learning.