Motivation
In machine learning and statistics, we often have to deal with structural data, which is generally represented as a table of rows and columns, or a matrix. A lot of problems in machine learning can be solved using matrix algebra and vector calculus. In this blog, I’m going to discuss a few problems that can be solved using matrix decomposition techniques. I’m also going to talk about which particular decomposition techniques have been shown to work better for a number of ML problems. This blog post is my effort to summarize matrix decompositions, as taught by Rachel Thomas and Xuemei Chen in the Computational Linear Algebra course at the University of San Francisco. This whole course is available for free as a part of fast.ai online courses. Here is the link to the introductory post by Rachel Thomas about the course.
Applications covered
- Background Removal
- Topic Modeling
- Recommendations using Collaborative Filtering
- Eigen Faces
List of more applications for the curious reader
- Data Compression
- CT Scan Reconstruction: Rachel’s notebook
- Linear Regression (Least Square Systems)
- Spectral Clustering: Blog by fellow USF student, Neerja Doshi
- Page Rank: Blog by fellow USF student, Alvira Swalin
- Moore-Penrose Pseudo Inverse
- Markov Chains
Background Removal
Automatic background removal has a number of use cases. For example, a Kaggle competition Carvana Image Masking Challenge was launched last year to develop an algorithm that automatically removes the photo studio background. For most E-commerce websites, photo background removal services are indispensable to increasing sales volume. Removing the background from photos highlights the products for E-commerce sites, like in the example below:

Separating the foreground from the background in videos also gives us the option to do something fun and interesting with the background. Mobile applications like Snapchat can potentially use this as an additional feature. State of the art background removal methods use neural nets for image segmentation, but for that we would need labeled data to train a neural net. This is where matrix decomposition can be used for background removal, as it provides a good baseline for unlabeled video data.
How to use matrix decomposition for background removal?
Singular Value Decomposition offers a neat way to separate the background and foreground from a video. The idea is to split a video into frames (which are just a collection of images), make each image into a 1-D vector, and horizontally stack into a matrix those 1-D vectors corresponding to each image. Then we do SVD to separate the foreground or background. If you had trouble with what I wanted to convey in the above 3 sentences, don’t worry! I’ll explain with visuals in the following section.
Step 1: Split video into frames based on some predefined frame per second

Step 2: Flatten each frame (convert to 1-D vector). Matrix of video with images as 1-D vector

Step 3: Do step 2 for all the frames and concatenate resultant 1-D vectors side by side
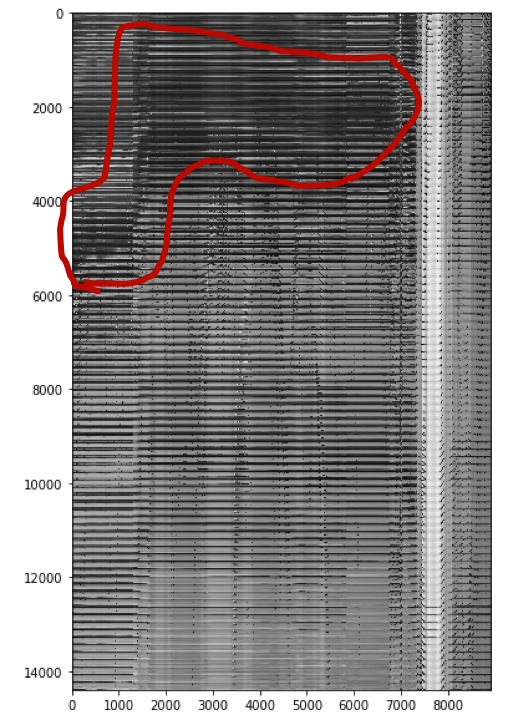
In the above matrix, most of the row vectors look almost the same, representing parts of an image which are constant across all frames (background). But there are some regions with wiggly patterns (marked in red) which look different. The idea is that the overall similar-looking pattern is the background, and the wiggly part is something that is not constant in different frames — like a walking pedestrian or a moving car.
Step 4: Decompose the matrix from step 3 using SVD. We get U, S, and V. Take the lower rank reconstruction of the original matrix by using only first k singular values of S. This gives us the background. The foreground is the difference between the original matrix and the lower rank matrix.
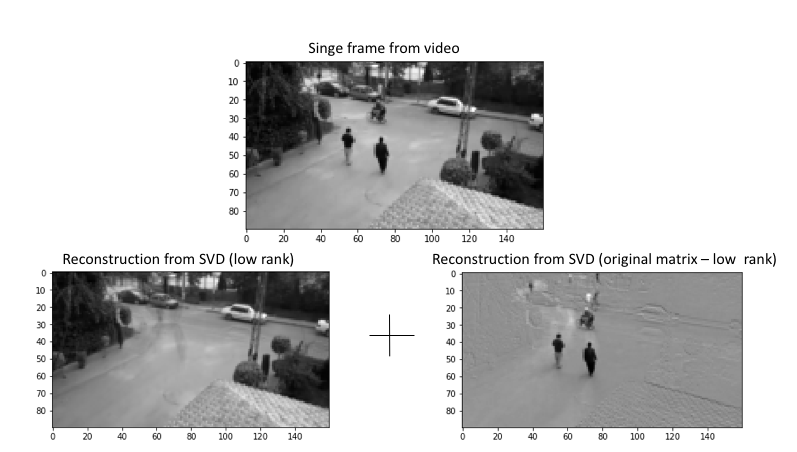
Here is the code: Jupyter notebook with code to do background removal using SVD
Topic Modeling
In machine learning and natural language processing, a topic model is a type of statistical model for discovering the abstract “topics” that occur in a collection of documents (wiki definition). Topic modeling is frequently used in text-mining tools for the discovery of hidden semantic structures in a text body.
A topic can be anything from a genre of songs to a species of animals. Given that a document is about a particular topic, one would expect particular words to appear in the document more or less frequently: “dog” and “bone” will appear more often in documents about dogs, “cat” and “meow” will appear in documents about cats, and “the” and “is” will appear equally in both. A document typically deals with multiple topics in different proportions; thus, in a document that is 10% about cats and 90% about dogs, there would probably be about 9 times more dog words than cat words.
One way to do topic modeling is to represent a corpus of text data in the form of a document-word matrix as shown below. Every column corresponds to a document and every row to a word. A cell stores the frequency of a word in a document — dark cells indicate high word frequencies. The resulting patterns are called “topics.”

We can do topic modeling in a number of ways. Two methods I’m going to discuss here in the context of matrix decompositions are Non-Negative Matrix Factorization (NMF) and Singular Value Decomposition (SVD).
General idea for the use of matrix decompositions for topic modeling: Consider the most extreme case — reconstructing the matrix using an outer product of two vectors. Clearly, in most cases we won’t be able to reconstruct the matrix exactly. But if we had one vector with the relative frequency of each vocabulary word out of the total word count, and one with the average number of words per document, then that outer product would be as close as we could get.
Now consider increasing the matrices to two columns and two rows. The optimal decomposition would now be to cluster the documents into two groups, each of which has as different distribution of words as possible to each other, but as similar as possible amongst the documents in the cluster. We’ll call those two groups “topics”. And we’d cluster the words into two groups, based on those which most frequently appear in each of the topics.
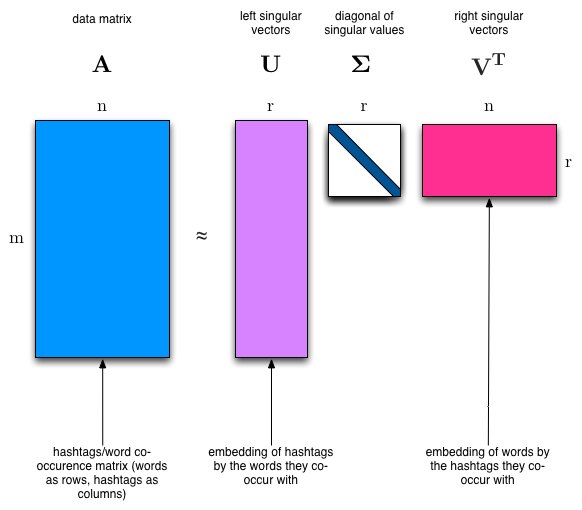
SVD: As discussed in the above paragraph, our goal in topic modeling is to separate out distinct topics from collection of text. We expect that the words that appear more frequently in one topic would appear less frequently in the other — otherwise that word wouldn’t make a good choice to separate out the two topics. In linear algebra terminology, we can say that we expect the topics to be orthogonal. The SVD factorizes a matrix into one matrix with orthogonal columns and one with orthogonal rows (orthogonal topics (along with a diagonal matrix, which contains the relative importance of each factor)). Below is an example of SVD where both U and VT are orthogonal matrices.
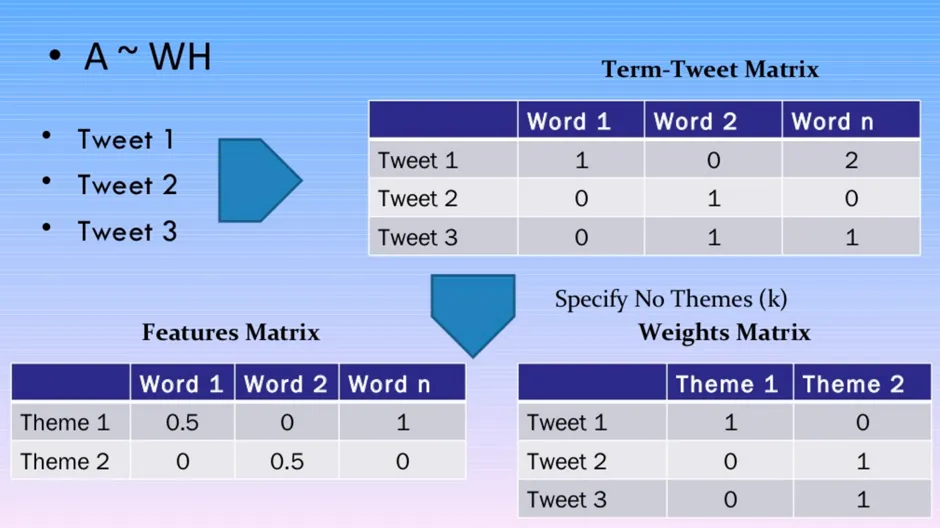
NMF: In SVD, we decomposed our matrices with the constraint that resultant matrices are orthogonal. Rather than constraining our factors to be orthogonal, another idea would be to constrain them to be non-negative. NMF is a factorization of a single non-negative matrix into two non-negative matrices. The reason behind the popularity of NMF is that positive factors are more easily interpretable and different kinds of data like pixel intensities, occurrence counts, user scores, stock market values are non-negative by nature.
For topic modeling, we use the Bag of Words representation of our documents and decompose it into the product of two non-negative matrices, as shown in the image below. We have to specify the number of unique topics we expect from the raw data.
Here is the code: Jupyter notebook with code to do topic modeling using SVD and NMF
Nice blog about topic modeling in sklearn using LDA and NMF
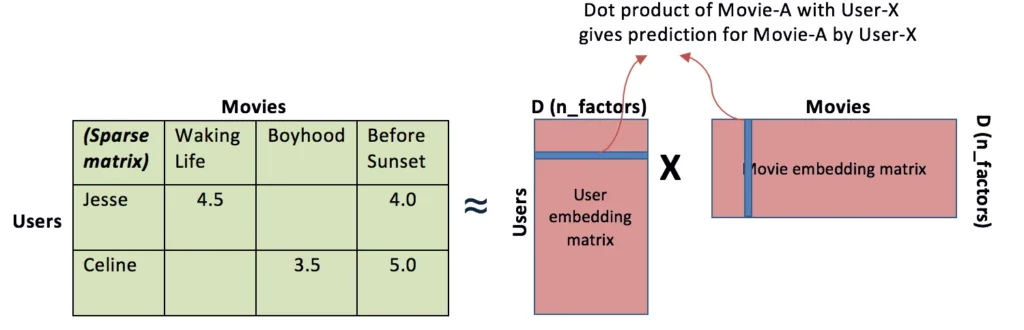
Recommendations using Collaborative Filtering
There are plenty of papers and articles out there talking about the use of matrix factorization for collaborative filtering. We can use Principal Component Analysis (PCA), Probabilistic Matrix Factorization (PMF), SVD, or NMF matrix decomposition techniques, depending on the specific use case.
In CF, past user behavior is analyzed in order to establish connections between users and items. This is then used to recommend an item to a user based on the opinions of other users. For most E-commerce websites like Amazon, the number of items and users are huge, which makes this challenging for CF algorithms. But matrix factorizations work well for sparse data.
I’ve discussed the use of matrix decompositions, plus some other techniques for collaborative filtering in another blog. I recommend reading that to know about different techniques used for collaborative filtering.
Eigen Faces
Eigen faces is the name given to a set of eigenvectors when they are used in the computer vision problem of human face recognition.
The idea of eigenfaces is this: there are a set of common abstract ingredients (technically eigenvectors) that are shared by all the faces we have in data. If this is true, then there must be a way to take the linear combination of those abstract ingredients to reconstruct the original image.
To find this out, we can use Principal Component Analysis (PCA) using SVD over the vector space of faces images. With PCA, we get a set of basis images (eigenvectors), and each individual image can be represented as a linear combination of those basis images. We can now do dimension reduction by allowing only the smaller set of basis images to represent the original training images.
As part of an assignment at USF, I did a PCA analysis on the headshots of students and faculty in a shared notebook (below). In the notebook, I’ve shown that we can reconstruct any image by using a few of the principle eigen faces. Eigen faces can also be used to see similarities among different faces.

Image reconstruction using top-k eigen faces
Original Image:

Reconstruction using eigenfaces:

Here is the code: Jupyter notebook with code to do eigenface decomposition
Conclusion
Even though matrix decomposition techniques like QR, SVD, NMF, PCA or Eigen Vector decomposition are very old, we’re still using them for many machine learning and statistics problems. In this post, I’ve attempted to explain a few of those problems in a non-technical manner. I hope you got a general idea for the types of machine learning applications of matrix decompositions.
About Me: I am currently working as a Research Scientist in Amazon Fraud Detector team at AWS. If you are interested in learning about ML in Fraud or in working with us, reach out to me through linkedin. You can read my other blogs here.
LinkedIn: https://www.linkedin.com/in/groverpr/
Twitter: https://twitter.com/groverpr4
References
Discuss this post on Hacker News and Reddit

Comments 0 Responses