At the recent TensorFlow Dev Summit, Google announced upcoming support on the TensorFlow platform for Swift. Their goal is to make it easier to use machine learning libraries and help catch more mistakes before running ML code.
Swift for TensorFlow — and some new Swift extensions planned for the upcoming Swift 4.2 release — will let you execute arbitrary Python code including scientific packages like NumPy, making it simple to port existing TensorFlow Python code to Swift.
While waiting for the availability of the first beta release of Swift 4.2 and the Google TFiwS framework, I thought it would be interesting to simulate some of the basics of TensorFlow and start implementing some easy Swift code to reproduce the dataflow graph — a key concept applied to some basic Swift tensor operations.
TensorFlow uses a dataflow graph to represent the computation in terms of the dependencies between individual operations expressed as nodes in a dataflow graph. This leads to a low-level programming model in which the developer first defines the dataflow graph and then creates a TensorFlow session to run parts of the graph across a set of local and remote devices.
TensorFlow uses a deferred execution methodology where developer first sets up a graph of operations, constants, and variables, and then later starts the execution, pumping in data continuously or in a batch.
Having described what a graph flow is, it’s important to define what a tensor is. A tensor is simply a generalization of vectors and matrices to higher dimensions. It’s used to represent the values for these constants, variables, and operations used in the graph flow.
TensorFlow internally represents tensors as n-dimensional arrays of base datatypes, typically floats. When using Python bindings, these n-dimensional arrays are typically mapped to NumPy arrays.
The key concept of TensorFlow is that it’s a way to defer the execution of a complex calculation defining a flow of constants, variables, and operations managing tensor values, usually represented in Python with NumPy n-dimensional arrays.
Swift n-dimensional array (Swift NumPy)
The idea of this brief tutorial is to simulate a TensorFlow graph of tensor operations on the Swift 4.1 world, without waiting for the availability of Python integration expected with the upcoming Swift 4.2 release.
In order to manage n-dimensional arrays in Swift, I chose to use one of the several NumPy-similar Swift Packages already available on GitHub. I opted in particular for NumSw available here:
Sample dataflow graph
In this tutorial, we won’t implement a real neural network model because, of course, that wouldn’t be just a “simulation,” and in order to do that we should first implement all the computation operations like activation, gradient descendent, and loss functions needed to really run a neural network.
Instead, we’ll build a super simple computation graph flow using three constants. Let’s name them a, b and c, and three very simple arithmetic operations on these constants:
- multiply: (a*b)
- sum: (b+c)
- subtract: (multiply — sum)
For the sake of simplification, we’ll also use vectors (one-dimensional tensors) to represent the values for the a, b, and c constants used for the operations of this simple flow (but of course, n-dimensional tensors could be easily used with here with Swift NumSw).
The following diagram illustrates the dataflow computation graph of this simple calculus, starting on the left from the constant nodes (a, b, and c) connected to the multiply (x) and sum (+) operation nodes, and finally to the subtract (-) node representing the final result for our calculus.
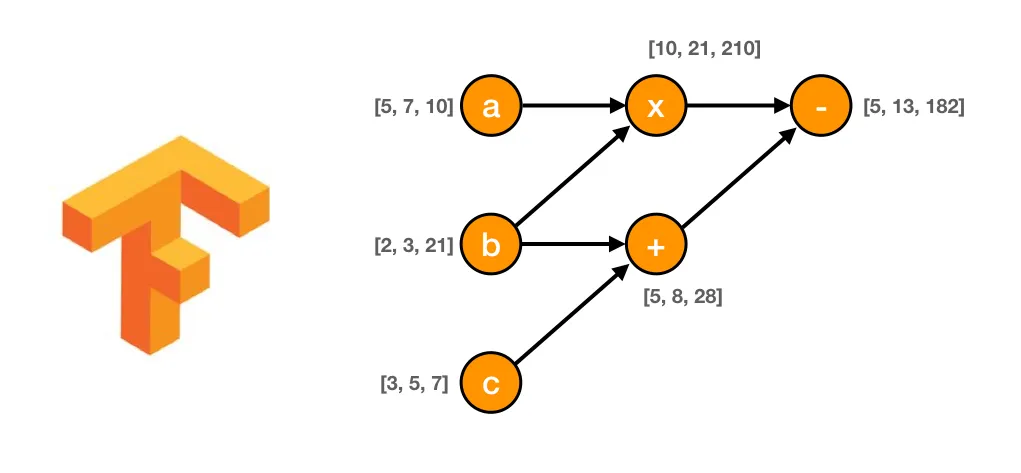
The key concept to note here is the dependencies between the nodes in terms of direct or indirect dependencies.
TensorFlow manage this dependency using the classic mathematical concept of a graph edge, managing on each node a list of (edges) connections to directly dependent node.
For example, we can see on the diagram below that the multiply (x) node directly depends on nodes a and b.
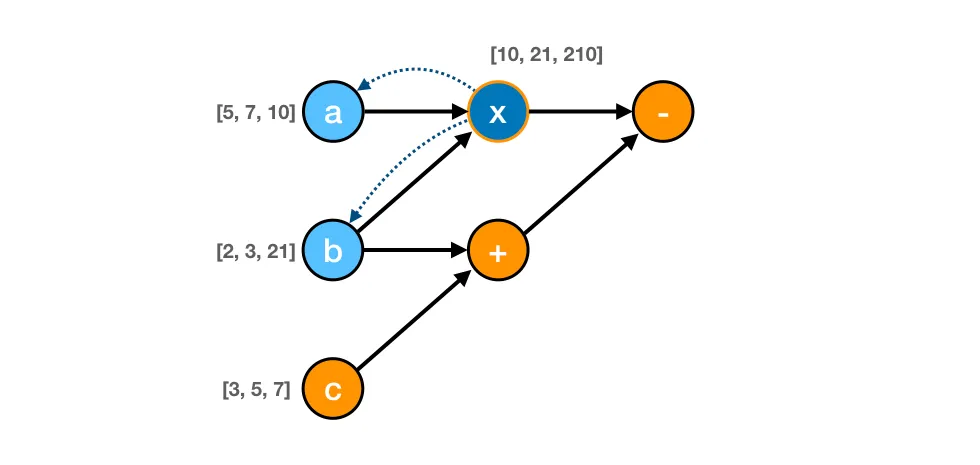
At the same time, the final subtraction (-) node depends directly on nodes x and + and indirectly on all other nodes (a, b, and c) as in the diagram below.
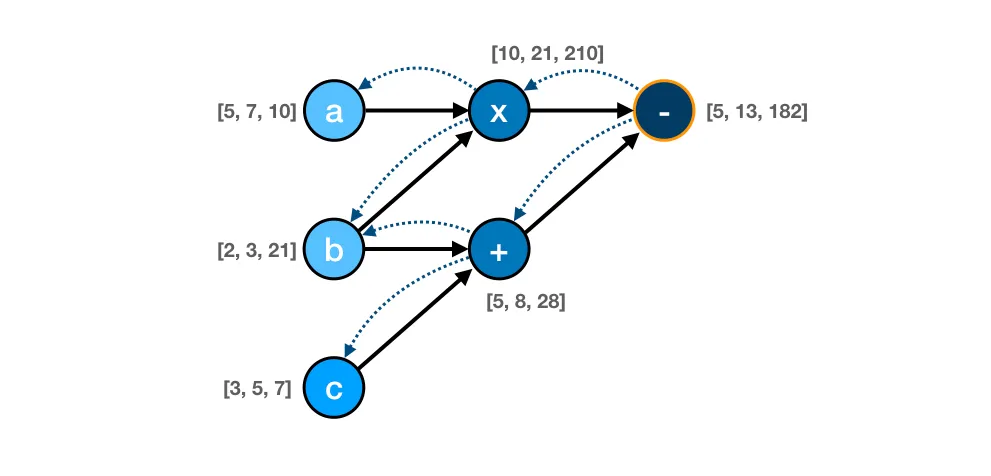
The adoption of this classic graph model lets TensorFlow run a super efficient lazy execution only of the part of the graph that is particularly needed to “run” a certain operation in the graph. It eventually distributes, in parallel, the execution of part of the graph on different nodes.
Python version
Here is a snippet of how to implement this simple graph calculus in Python using the TensorFlow API.
import tensorflow as tf
import numpy as np
a = tf.constant(np.array([5, 7, 10]))
b = tf.constant(np.array([2, 3, 21]))
c = tf.constant(np.array([3, 5, 7]))
d = a * b # tf.multiply(a,b)
e = c + b # tf.add(c,b)
f = d - e # tf.subtract(d,e)
sess = tf.Session()
outs = sess.run(f)
sess.close()
As you may see running this code, the d, e, and f TensorFlow variables are just placeholders for the output of “running” the graph operations multiply (*), add (+), and subtract (-). The real values for these variables won’t be assigned until the TensorFlow graph session is executed, running the entire graph or just part of it.
Calling the TensorFlow run() method for the f variable pointing to the final node subtract (-) operation of our graph signals TensorFlow to run the entire graph because, as we’ve already seen, the (-) node depends on all the previous nodes.
Swift version
The goal for this tutorial is to port to Swift the same Python code above, with the only exception of using NumSw instead of NumPy, and to simplify the TensorFlow Session usage, since we clearly don’t have the goal to scale up the graph execution on different nodes.
import Foundation
import TensorFlow
import numsw
var tf = TensorFlow()
let a = tf.constant(NDArray<Float>(shape: [3], elements: [5, 7, 10]))
let b = tf.constant(NDArray<Float>(shape: [3], elements: [2, 3, 21]))
let c = tf.constant(NDArray<Float>(shape: [3], elements: [3, 5, 7]))
var d = a * b // tf.multiply(a,b)
var e = c + b // tf.add(c,b)
var f = d - e // tf.subtract(d,e)
tf.run(f)The Swift code for executing this graph calculus really looks a lot like the code we’ve written in Python thanks to Swift’s support for operator overloading.
Swift graph operation source code
The source code below implements in Swift a simple Graph model to simulate the TensorFlow dataflow graph deferred logic and the basic functionality to run a node. It also adds simple operations in a very natural way using operator overloading.
A generic Node class defines in particular the basic TensorFlow interface, and specialized inherited classes implement specific behaviors for tensor constants and variables and the basic arithmetic tensor operations (Add, Subtract, Multiply, Divide) supported in this simulation.
Finally, a TensorFlow class implements, using some shortcuts, the concept of TensorFlow session in an implicit way, managing a unique array for all nodes in the graph.
import Foundation
import numsw
class Node {
var tf: TensorFlow?
var edges: [Node]
init(tf: TensorFlow? = nil) {
self.tf = tf
self.edges = [Node]()
}
func run() -> NDArray<Float>? {
return nil
}
static func +(left: Node, right: Node) -> Node {
let x = Add(left, right)
left.tf?.nodes.append(x)
return x
}
static func -(left: Node, right: Node) -> Node {
let x = Subtract(left, right)
left.tf?.nodes.append(x)
return x
}
static func *(left: Node, right: Node) -> Node {
let x = Multiply(left, right)
left.tf?.nodes.append(x)
return x
}
static func /(left: Node, right: Node) -> Node {
let x = Divide(left, right)
left.tf?.nodes.append(x)
return x
}
}
class Constant : Node {
var result: NDArray<Float>?
init(_ value: NDArray<Float>, tf: TensorFlow? = nil) {
self.result = value
super.init(tf: tf)
}
override func run() -> NDArray<Float>? {
return result
}
}
class TwoOperandNode : Node {
var result: NDArray<Float>?
init(_ node1: Node, _ node2: Node, tf: TensorFlow? = nil) {
super.init(tf: tf)
self.edges.append(node1)
self.edges.append(node2)
}
}
class Add : TwoOperandNode {
override func run() -> NDArray<Float>? {
guard self.edges.count == 2, let a = self.edges[0].run(), let b = self.edges[1].run() else { return nil }
return a + b
}
}
class Subtract : TwoOperandNode {
override func run() -> NDArray<Float>? {
guard self.edges.count == 2, let a = self.edges[0].run(), let b = self.edges[1].run() else { return nil }
return a - b
}
}
class Multiply : TwoOperandNode {
override func run() -> NDArray<Float>? {
guard self.edges.count == 2, let a = self.edges[0].run(), let b = self.edges[1].run() else { return nil }
return a * b
}
}
class Divide : TwoOperandNode {
override func run() -> NDArray<Float>? {
guard self.edges.count == 2, let a = self.edges[0].run(), let b = self.edges[1].run() else { return nil }
return a / b
}
}
class TensorFlow {
var nodes = [Node]()
func constant(_ v: NDArray<Float>) -> Node {
let x = Constant(v)
nodes.append(x)
return x
}
func add(_ n1: Node, _ n2: Node) -> Node {
let x = Add(n1, n2)
nodes.append(x)
return x
}
func subtract(_ n1: Node, _ n2: Node) -> Node {
let x = Subtract(n1, n2)
nodes.append(x)
return x
}
func multiply(_ n1: Node, _ n2: Node) -> Node {
let x = Multiply(n1, n2)
nodes.append(x)
return x
}
func divide(_ n1: Node, _ n2: Node) -> Node {
let x = Divide(n1, n2)
nodes.append(x)
return x
}
func run(_ n: Node) -> NDArray<Float>? {
return n.run()
}
}Full source code for this tutorial is available at:
Discuss this post on Hacker News

Comments 0 Responses